解答题
设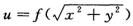
且二阶连续可导，又
,求f(x).
您可能感兴趣的题目
-
设Φ1(x),Φ2(x),Φ3(x)为二阶非齐次线性方程y“+a1(x)y’+a2(x)y=f(x)的三个线性无关解，则该方程的通解为（ ）。 C1[Φ1(x)+Φ2(x)]+C2Φ3(x) C1[Φ1(x)-Φ2(x)]+C2Φ3(x) C1[Φ1(x)+Φ2(x)]+C2[Φ1(x)-Φ3(x)] C1Φ1(x)+C2Φ2(x)+C3Φ3(x),其中C1+C2+C3=1
-
设y=y(x)满足[*],且有y(1)=1,则[*]=________.
-
以y=C1ex+ex(C2cosx+C3sinx)为通解的三阶常系数齐次线性微分方程为________.
-
设有微分方程y’-2y=Φ(x),其中[*],求在（-∞，+∞）内连续的函数y(x)，使其在（-∞，1）及（1，+∞）内都满足所给的方程，且满足条件y(0)=0.
-
设y=y(x)二阶可导，且y’≠0,x=x(y)是y=y(x)的反函数。
-
位于上半平面的上凹曲线y=y(x)过点（0,2）,在该点处的切线水平，曲线上任一点（x,y)处的曲率与[*]及1+y’2之积成反比，比例系数为[*],求y=y(x).
-
设曲线L1、L2皆过点（1,1），曲线L1在点（x,y）处纵坐标与横坐标之商的变化率为2，曲线L2在点（x,y)处纵坐标与横坐标之积的变化率为2，求两曲线所围成区域的面积。
-
飞机以匀速v沿y轴正向飞行，当飞机行至O时被发现，随即从x轴上点（x0,0)处发射一枚导弹向飞机飞去（x0﹥0），若导弹方向始终指向飞机，且速度大小为2v.
-
质量为1g的质点受外力作用作直线运动，外力和时间成正比，和质点的运动速度成反比，在t=10s时，速度等于50cm/s,外力为39.2cm/s2,问运动开始1min后的速度是多少？
-
设A从原点出发，以固定速度v0沿y轴正向行驶，B从（x0,0)出发（x0<0),以始终指向A的固定速度v1朝A追去，求B的轨迹方程。
-
设f(x)为偶函数，且满足f’(x)+2f(x)-[*]=-3x+2,求f（x).
-
设函数f(x)（x≥0)可微，且f(x)﹥0,将曲线y=f(x),x=1,x=a(a﹥1)及x轴所围成的平面图形绕x轴旋转一周得旋转体体积为[*].若f(1)=[*].
-
用变量代换x=lnt将方程[*]化为y关于t的方程，并求原方程的通解。
-
某人的食量是2500卡/天（1卡=4.1868焦），其中1200卡/天用于基本的新陈代谢，在健身运动中，他所消耗的为16卡/千克/天乘以他的体重。假设以脂肪形式存储的热量百分之百有效，而一千克脂肪含热量10000卡，求该人体重怎么随时间变化。
-
设函数f（x)二阶连续可导，f(0)=1,且有[*],求f(x).
-
设y(x)是微分方程y“+(x-1)y’+x2=ex，满足初始条件y(0)=0,y’(0)=1的解，则[*]( ). 等于1 等于2 等于0 不存在
-
微分方程yy“-2y(y’)2=0的通解为________.
-
设[*]且二阶连续可导，又[*],求f(x).
-
某湖泊水量为V,每年排入湖泊中内含污染物A的污水量为[*],流入湖泊内不含A的水量为[*],流出湖的水量为[*].设1999年底湖中A的含量为5m0,超过国家规定指标，为了治理污染，从2000年初开始，限定排入湖中含A污水的浓度不超过[*],问至多经过多少年，湖中污染物A的含量降到m0以内（设湖中A的浓度是均匀的）？
